Associação de Resistores em Paralelo - Cálculos: Resistor Equivalente, Corrente, Potência!

Associação de Resistores em Paralelo - Cálculos: Resistor Equivalente, Corrente, Potência!

Associação de Resistores em Paralelo

Na Associação de Resistores em Paralelo, os resistores estão interligados de forma tal que, a ligação de todas as resistências esteja conectada respectivamente a cada terminal de cada resistor do conjunto associado, como mostrado na Figura 2 abaixo.

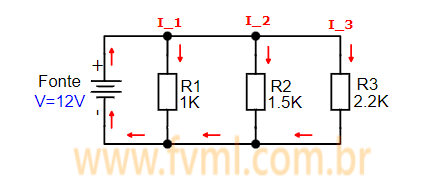Fig. 2 - Associação de resistores Paralelo

A Corrente Elétrica em todos os resistores, podem diferir, já que existem vários caminhos para a corrente percorrer, e essa corrente depende da resistência elétrica de cada resistor.

A Tensão Elétrica que percorre todo circuito é sempre a mesma em cada nó no circuito com resistores em paralelo.

Você pode se interessar também:

• Segunda Lei de Ohm: O que é? Fórmula Prática e Aplicação
• Associação de Resistores em Série - Cálculos: Resistor Equivalente, Corrente, Tensão e Potência!
• Associação de Resistores - Em Série, em Paralelo e Mista!
• O que São Resistores? Como eles trabalham? Tipos de Resistores e suas Definições!
• DIAC - O que é, e como Funciona?
• Reguladores de Tensão Lineares. O que são e como funcionam!
• Como fazer leitura de Capacitores de Poliéster e Cerâmico Corretamente
• O que são Varistores? Como Funcionam? Para que Servem?
• Como funcionam os Relés, quais suas características, e suas aplicações!!!
  

No nosso circuito exemplo, utilizamos as seguintes configurações:

• Fonte de alimentação: VFonte = 12V
• Resistores de: R1 = 1KΩ, R2 = 1.5KΩ, R3 = 2.2KΩ

 Calcularemos:

• A Resistência Equivalente
• A Corrente em cada Resistor
• A Tensão em nos Resistores
• A potência dissipada em cada Resistor
  

Cálculo de Resistência Equivalente

Como em nosso exemplo utilizamos três resistores diferentes, podemos utilizar a soma algébrica apresentada na fórmula matemática abaixo, para realizarmos o somatório e chegarmos ao Resistor Equivalente “REQ”, como ilustrado na Fórmula abaixo.

Fórmula Geral:

Aplicando os valores dos resistores; R1=1KΩ; R2=1.5KΩ; e R3=2.2KΩ; na fórmula geral, o resultado desse somatório ficaria assim:

E o resultado da Resistência Equivalente foi 473,93Ω, sendo assim, o resistor equivalente comercial mais próximo, será o resistor de 470Ω. 

Cálculo da Corrente nos Resistores!

A corrente total, Itotal que entra em um circuito resistivo paralelo é a soma de todas as correntes individuais que fluem em todos os ramos paralelos.

No entanto, nem sempre a quantidade de corrente que flui através de cada ramo paralelo é a mesma, já que a corrente em cada nó, e dependente do valor resistivo de cada ramo, conforme determina a Lei de Ohms.

Existem basicamente 2 métodos que podemos utilizar para calcular a corrente que flui no circuito em paralelo:

Primeiro método: Através do cálculo Individual em cada ramo.

A Lei Kirchhoff das Correntes, afirmam que: A corrente total que sai de um circuito é igual à que entra no circuito, ou seja; nenhuma corrente é perdida. Sendo assim, a corrente total que flui no circuito é dada por:

Fórmula Geral:

Usando a Lei de Ohm, podemos calcular a corrente que flui através de cada resistor paralelo como mostrado na fórmula das correntes acima, a soma das correntes de cada resistor independente, ficando assim:

Fórmula Geral:

V = R * I

• Aplicando a fórmula no resistor R1 = 1KΩ:
• IR1 = Vfonte / R1 = 12V / 1000 = 0.012
• IR1 = 12mA
  
  
• Aplicando a fórmula no resistor R2 = 1.5KΩ:
• IR2 = Vfonte / R2 = 12V / 1500 = 0.008
• IR2 = 8mA
  
  
• Aplicando a fórmula no resistor R3 = 2.2KΩ:
• IR3 = Vfonte / R3 = 12V / 2200 = 0.005
• IR3 = 5mA

Sabendo a corrente em cada ramo resistivo, podemos calcular a corrente que flui em todo circuito utilizando a Lei de Kirchhoff, com as somas das correntes:

• IToral = 12mA + 8mA + 5mA
• ITotal = 25mA 
  

Segundo método: Através do cálculo do Resistor Equivalente.

Usando a Lei de Ohm, podemos calcular a corrente que flui através do resistor equivalente, como já foi calculado e já sabemos o valor do resistor equivalente, é só colocarmos na fórmula e observar o resultado, ficando assim:

Fórmula Geral:

• V = R * I

Aplicando em nosso Circuito:

• Itotal = Vfonte / Requivalente
• Itotal = 12 / 470
• Itotal = 0.025A ou 25mA
  

Cálculo da Potência dos Resistores

Para calcular a Potência dos Resistores, podemos utilizar os resultados dos métodos já descritos acima. Já calculamos a corrente total do circuito e a corrente em cada ramo do circuito com os dois métodos dado, podemos utilizar a cálculo da corrente total, ou a corrente independente em cada ramo resistivo.

Utilizaremos a Lei de Ohms para calcularmos a potência consumida por cada resistores:

Fórmula Geral:

• P = V * I => Para calcular a potência em cada resistor
  

Aplicando a fórmula para medir a potência no resistor R1:

• PR1 = V * IR1
• PR1 = 12V * 12mA
• PR1 = 144mW 

Aplicando a fórmula para medir a potência no resistor R2:

• PR2 = VR2 * IR2
• PR2 = 12V * 8mA
• PR2 = 96mW 

Aplicando a fórmula para medir a potência no resistor R3:

• PR3 = VR3 * IR3
• PR3 = 12V * 5mA
• PR3 = 60mW 
  

Para que não está familiarizado com a potência dos resistores comerciais, segue abaixo os três resistores padrões comerciais que temos, de baixa potência:

• Resistor de 1/8W = 1000/8 = 125mW
• Resistor de 1/4W = 1000/4 = 250mW
• Resistor de 1/2W = 1000/2 = 500mW
  

Conclusão

Aprendemos que em Associação de Resistores em Paralelo:

• Para calcular a Resistência Equivalente, podemos utilizar a fórmula matemática da soma algébrica e chegarmos ao Resistor Equivalente "REQ".
• A corrente que percorre todo o circuito, sempre é dividida em cada ramo resistivo. 
• Para calcular a corrente total do circuito utilizamos a Lei de Kirchhoff e a Lei de Ohms.
• A tensão que percorre todo circuito, é sempre igual em todos os resistores, ou seja, todos recebem o mesmo potencial elétrico.
• A potência de um circuito elétrico pode ser calculada como sendo P = V * I, onde P é a potência em Watts, V é a tensão em Volts e I é a corrente elétrica em Amperes.
• O valor da resistência Equivalente sempre é menor que a menor resistência em todos os ramos.

E por hoje é só, espero que tenhamos alcançado suas expectativas!

Agradecemos por visitar o nosso blog e esperamos tê-lo(a) novamente por aqui em breve. Não deixe de conferir nossos outros conteúdos sobre tecnologia e assuntos variados. 

Se inscreva no nosso Blog! Clique Aqui — FVM Learning!

Nos ajude a divulgar nosso trabalho, compartilha nas redes sociais, Facebook, Instagram, nos grupos de WhatsApp, uma simples atitude sua, faz com que cresçamos juntos e melhoremos o nosso trabalho!

Forte abraço!
Deus vos Abençoe!
Shalom.